堆
今天来讲一下 堆(优先队列)。
应用场景
求最值问题。
算法思路
模板题:P3378 【模板】堆
。
带入
让我们复习一下学过的最值问题。
( 为数组的长度)
- 暴力 时间复杂度
- 线段树 用不了(无法增删)
- 单调队列 用不了(太惨了)
- 倍增(ST表) 用不了(只能处理静态的区间最值)
很显然,没有算法可以AC这道题,我们需要新的算法。
处理
我们使用一种叫 堆(优先队列)的数据结构。
堆是一棵二叉树,有大根堆和小根堆。
大根堆:父节点 子节点。
小根堆:父节点 子节点。
此外,堆还是一个完全二叉树。
那堆如何进行增删查呢?
(虽然题目中需要使用小根堆,但这里为了讲解需要,下面都是大根堆)
增
这是一个大根堆。
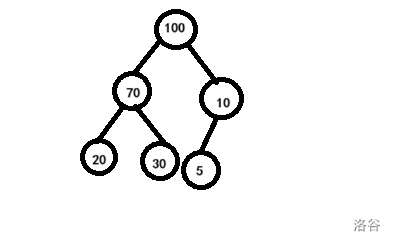
我们增的步骤如下(例如插入20)。
- 先把数插在最后面。
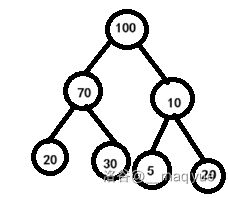
- 再和父节点交换。
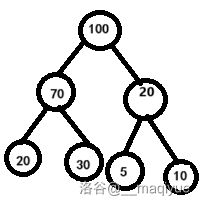
查
由于堆的约束,堆没有太多规律,所以查只会查根节点。
例如上面这个堆查询的结果就是 。
删
跟查一样,只能删除根节点,那又该如何操作呢?
- 当然先把根节点给删掉。
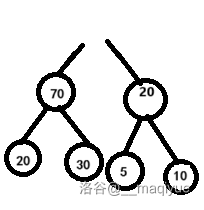
- 把最后一个节点当做根节点。
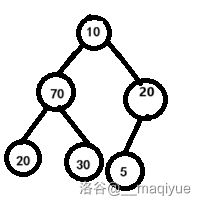
- 选择根节点的子节点中较大(如果是小根堆就较小)的值进行比较。
因为 ,所以 要和 进行比较,不满足,交换。
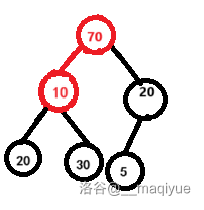
因为 ,所以 要和 进行比较,不满足,交换。
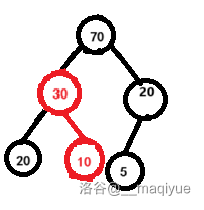
因为 已经到了最低端,没有子节点,所以结束。
我们在执行步骤 3 的时候,发现执行完最后一次后,这棵树依然满足堆的特点,为什么呢?
这就要跟为什么要选择最大值进行比较有关系了。
我们试试用较小的值交换。
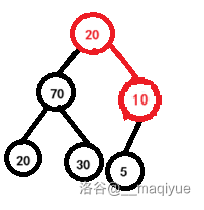
我们发现由于 这个堆不是大根堆,而最大值改除了 没有其他问题,所以应该找最大的比较。
(你说最大值比较不是有 的问题吗,纯属巧合)
回答第一个问题,因为每次都在尝试把这个堆变成正常的堆,所以结束了,堆自然就正确了,而且每次最多只有可能有 的问题,换完就没有错误了。
代码实现
(这里按题目是小根堆)
定义变量和存储
如何存储一棵树,很简单,根节点编号为 ,编号为 的点左节点的编号为 ,右节点的编号则为 。
将这些升级为速度更快的位运算就为 p << 1 和 p << 1 | 1。
题目的数据范围是 ,堆又是一个完全二叉树,所以数组只用开 就够了。
我们还需要一个 ,代表当前数组的长度。
当然,我们还要一个题目中给的数 。
int tre[1000010],l,n;增
我们按照原先增的顺序进行操作。
先在堆的尾部加上值(添加的值为 )。
tre[++l] = x;再和父节点交换。
if(tre[l] > tre[l / 2])//注意,如果tre[l]是右节点的话/2会向下取整,所以不用担心
swap(tre[l],tre[l / 2]);我们知道,这个过程不止一次,所以需要一个 while 循环。
int p = l;
while(p > 1 && tre[p] < tre[p / 2])
swap(tre[p],tre[p / 2]),p /= 2;//注意,如果交换了,p要变为自己的父节点最后把它封装成函数。
void push(int x)
{
tre[++l] = x;
int p = l;
while(p > 1 && tre[p] < tre[p / 2])//没有到顶
swap(tre[p],tre[p / 2]),p /= 2;
}查
直接用返回堆顶的值就行了。
int top(){return tre[1];}删
按照步骤原先删的步骤进行。
先把原来的值覆盖。
tre[1] = tre[l--];//注意要l--再像增一样弄。
int p = 1,q = p * 2;//p始终维护一个子节点最小的值
while(q <= l)//还有子节点
{
if(q + 1 <= l && tre[q + 1] < tre[q]) q++;
if(tre[p] > tre[q]) swap(tre[p],tre[q]);
else break; //如果不用交换就满足了,直接退出
p = q,q = p * 2;//更新
}封装成函数。
void pop()
{
tre[1] = tre[l--];
int p = 1,q = p * 2;
while(q <= l)
{
if(q + 1 <= l && tre[q + 1] < tre[q]) q++;
if(tre[p] > tre[q]) swap(tre[p],tre[q]);
else break;
p = q,q = p * 2;
}
}最终代码
#include<bits/stdc++.h>
using namespace std;
int tre[1000010],l,n;
void push(int x)
{
tre[++l] = x;
int p = l;
while(p > 1 && tre[p] < tre[p / 2])
swap(tre[p],tre[p / 2]),p /= 2;
}
int top(){return tre[1];}
void pop()
{
tre[1] = tre[l--];
int p = 1,q = p * 2;
while(q <= l)
{
if(q + 1 <= l && tre[q + 1] < tre[q]) q++;
if(tre[p] > tre[q]) swap(tre[p],tre[q]);
else break;
p = q,q = p * 2;
}
}
int main()
{
cin >> n;
while(n--)
{
int op,x;
scanf("%d",&op);
if(op == 1) scanf("%d",&x),push(x);
else if(op == 2) cout << top() << endl;
else pop();
}
return 0;
}STL 做法
堆也被 STL 封装成模版了。
模版名叫 priority_queue。
用法是这样的。
priority_queue<你的类型> q;//默认大根堆如果你要小根堆请这样输入。
priority_queue<你的类型,vector<你的类型>,greater<你的类型>> q;//注意最后的>>,中间不加空格并且不开C++11会以为是右移比如我有一个结构体用来封装请在中间插入这样一个函数。
bool operator < (const &结构体名称 y) const
{
你的做法
}它拥有 push,top,pop 等函数,用法如下。
q.push(x);//向堆里插入x
q.top();//获取堆首的值
q.pop();//删除堆首最终代码:
#include<bits/stdc++.h>
using namespace std;
int main()
{
priority_queue<int, vector<int>, greater<int>> q;
int n;
cin >> n;
while (n--)
{
int op, x;
scanf("%d", &op);
if (op == 1) scanf("%d", &x), q.push(x);
else if (op == 2) cout << q.top() << endl;
else q.pop();
}
return 0;
}好题推荐
| 题号 | 题目 | 难度 |
|---|---|---|
| P3378 | 【模板】堆 | 普及− |
| P1801 | 黑匣子 | 普及+/提高 |
| P1168 | 中位数 | 普及+/提高 |
| P1752 | 点菜 | 省选/NOI− |
| P2048 | [NOI2010] 超级钢琴 | 省选/NOI− |
| P3644 | [APIO2015] 巴邻旁之桥 | 省选/NOI− |
修改记录
11/24 修改了句子末尾应添加句号,且全文使用的句号应一致的问题。