Tarjan
今天来讲一下 Tarjan。
应用场景
割点缩点。
dfn 和 low
思路
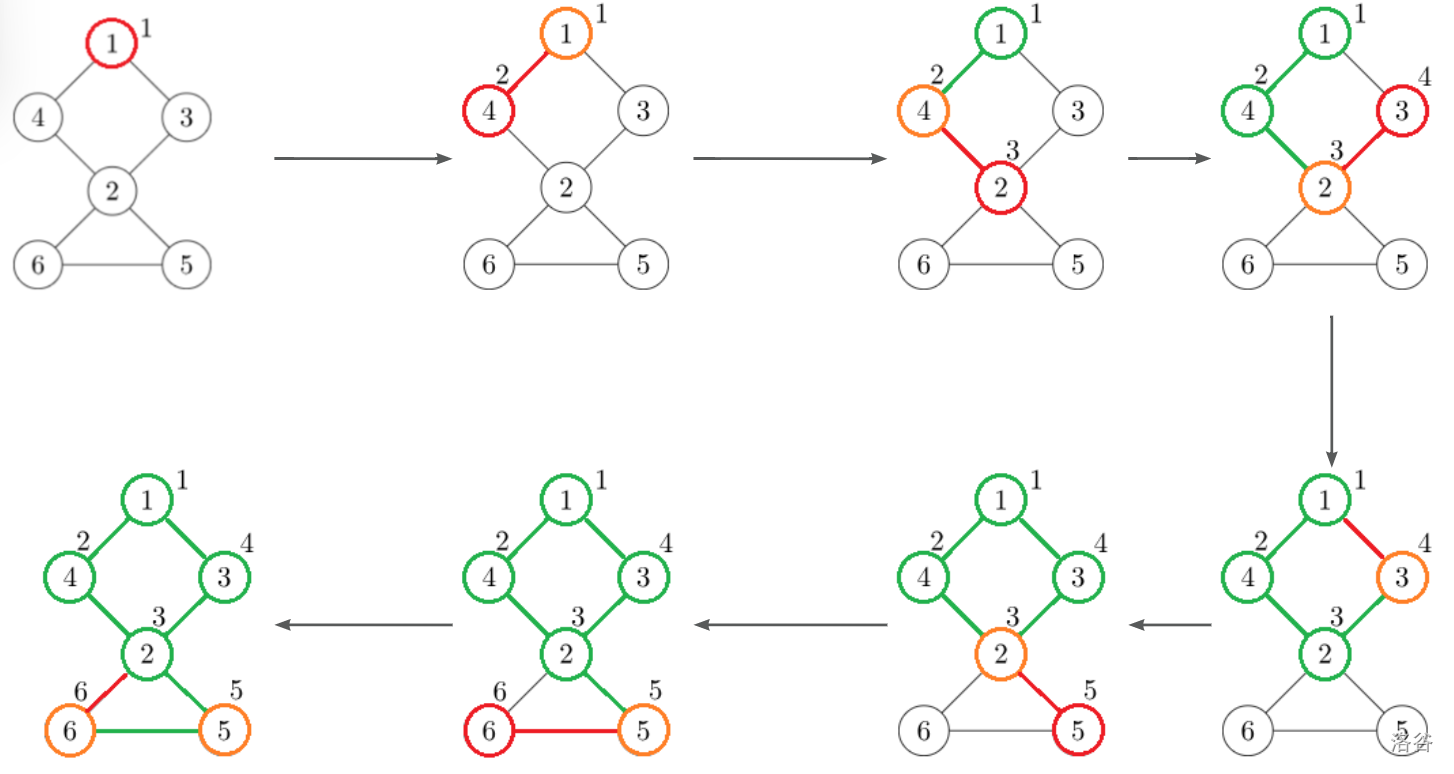
先上一个图:
Tarjan是这样操作的:
首先,用dfs遍历图,按照遍历的顺序给每个点打上时间戳(为dfn),每个点的时间戳如下(每个点右上角的数字为该点的 dfn):
再定义一个数组 low,为不经过其父亲能到达的最小的时间戳。
什么意思?其实不懂也没有关系 本蒟蒻开始读也没读懂。
换一个说法,就是不经过从起点到这个点已经经过的点,可以走到的最小时间戳。
步骤如下:(每个点右上角为该点的 dfn,low)
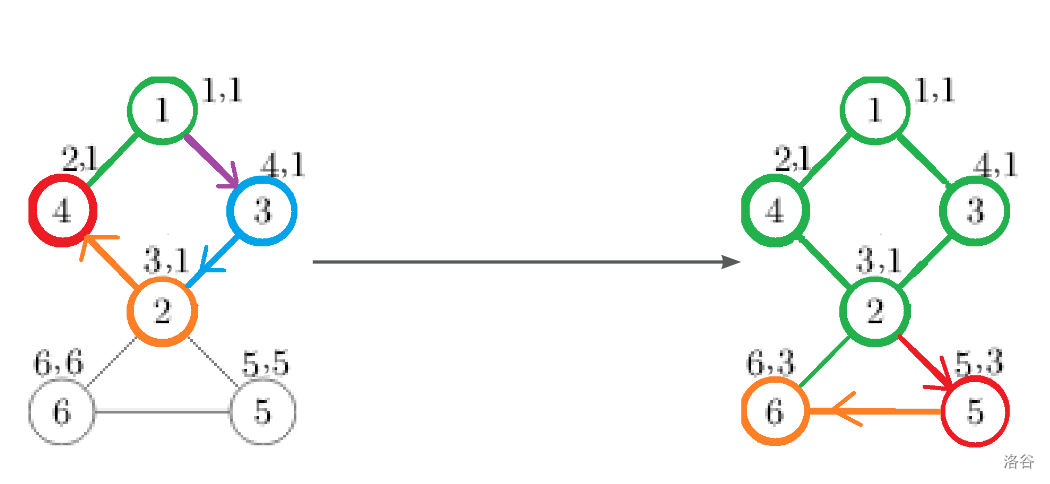
实现
更新 low
如何实现更新 low?
我们发现,上图的点有 种 low :
- 是下一个节点的
dfn(图中的 ) - 是下一个节点的
low(图中的 ) - 为 (图中的 )
分别满足以下条件:
- 下一个节点是自己的父节点(已经经过的点)
- 下一个节点是自己的子节点(还未到达过的点)
- 是图的根
实现代码:
//u为当前边的起点,v为终点,root为根
if (!dfn[u])
low[u] = min(low[u], low[v]);
else if (u != root)
low[u] = min(low[u], dfn[v]);
else
low[u] = 1;我们发现当点是根时,不需要特判,因为 是图中最小的 low 和 dfn。
//u为当前边的起点,v为终点,root为根
if (!dfn[u])
low[u] = min(low[u], low[v]);
else
low[u] = min(low[u], dfn[v]); 实现初始化 dfn 和 low
因为可能是非连通图,所以可能有多个根,调用时的代码如下:
int main()
{
//……
for (int i = 1; i <= n; i++)
if (!dfn[i])
tarjan(i, i);
//……
return 0;
}用链式前向星存图的童鞋看这:
//hd[i]为最后一条以i点为起点的边的编号
//e[i].v为编号为i这条边的终点
//e[i].nxt为下一条以i这条边的起点为起点的边
void tarjan(int u,int root)
{
dfn[u] = low[u] = ++cnt;
for (int i = hd[u]; i; i = e[i].nxt)
{
int v = e[i].v;
if (!dfn[u])
{
tarjan(v, root);//因为这个点还未更新
low[u] = min(low[u], low[v]);
}
else
{
low[u] = min(low[u], dfn[v]);
}
}
}
//……
int main()
{
//……
for (int i = 1; i <= n; i++)
if (!dfn[i])
tarjan(i, i);
//……
return 0;
}用 vector 存图的童鞋看这:
//e[u][i]为起点为u的第i条边的终点
void tarjan(int u,int root)
{
dfn[u] = low[u] = ++cnt;
for (auto v : e[u])
{
if (!dfn[u])
{
tarjan(v, root);//因为这个点还未更新,所以遍历这个点
low[u] = min(low[u], low[v]);
}
else
{
low[u] = min(low[u], dfn[v]);
}
}
}
//……
int main()
{
//……
for (int i = 1; i <= n; i++)
if (!dfn[i])
tarjan(i, i);
//……
return 0;
}割点
判定割点
那满足什么是割点呢?
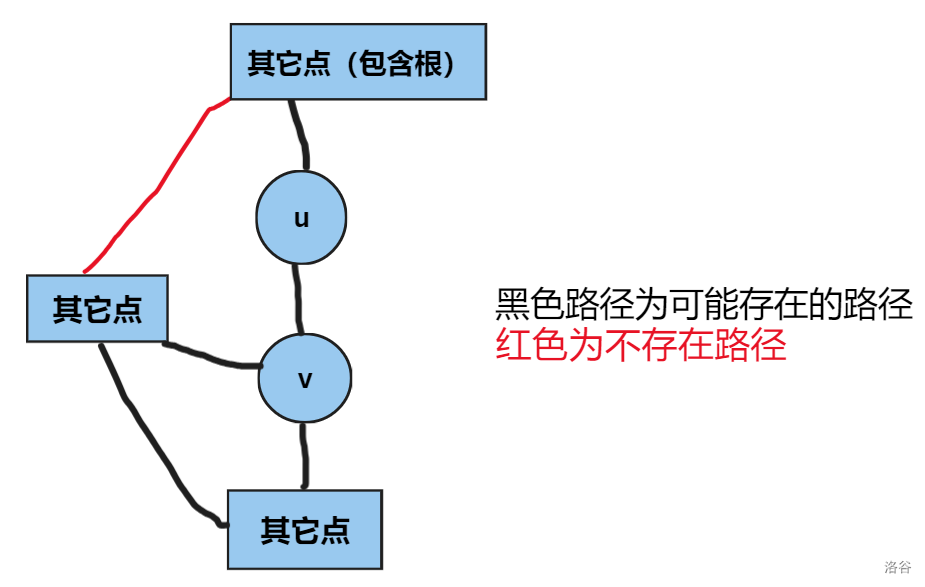
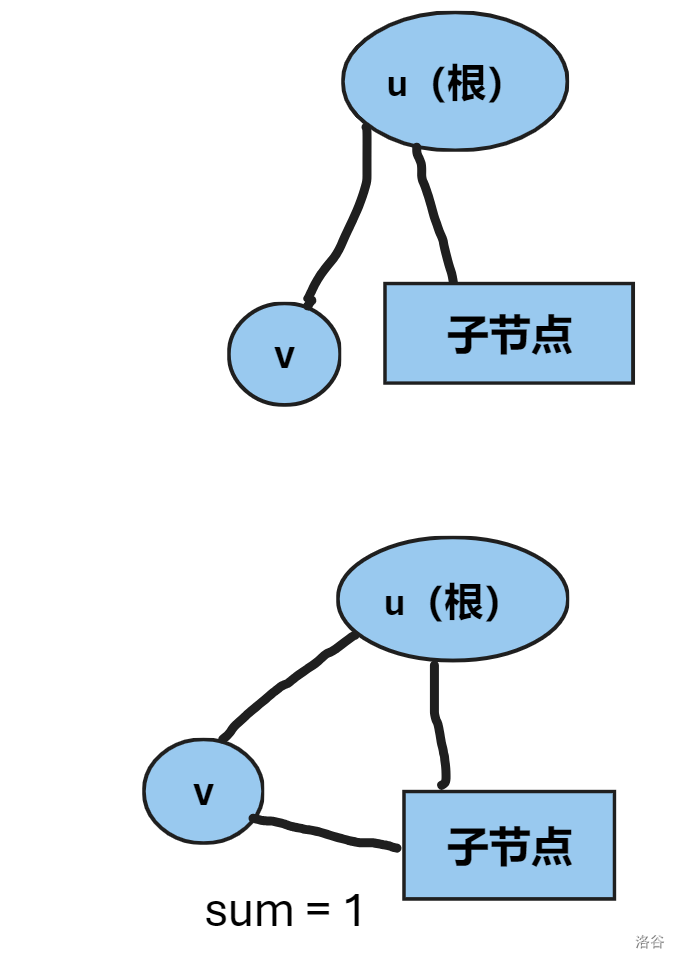
( 为当前边的起点, 为终点, 为根, 为子节点数量)
割点满足
情况是这样的:
实现
用链式前向星存图的童鞋看这:
#include<bits/stdc++.h>
using namespace std;
const int N = 20010, M = 100010;
int n, m, hd[N], tot, dfn[N], low[N], cnt;
bool iscut[N];//为i这个点是否为割点
struct edge {
int v, nxt;
}e[M << 1];
void add_edge(int u, int v)
{
e[++tot] = edge{ v,hd[u] };
hd[u] = tot;
e[++tot] = edge{ u,hd[v] };
hd[v] = tot;
}
void tarjan(int u, int root)
{
dfn[u] = low[u] = ++cnt;
int sum = 0;
for (int i = hd[u]; i; i = e[i].nxt)
{
int v = e[i].v;
if (!dfn[v])
{
sum++;//子节点+1
tarjan(v, root), low[u] = min(low[u], low[v]);
if (u != root && dfn[u] <= low[v]) iscut[u] = true;
}
else
low[u] = min(low[u], dfn[v]);
}
if (u == root && sum > 1) iscut[u] = true;
}
int main()
{
cin >> n >> m;
for (int i = 1, u, v; i <= m; i++)
scanf("%d%d", &u, &v), add_edge(u, v);
for (int i = 1; i <= n; i++)
if (!dfn[i])
tarjan(i, i);
int ans = 0;
for (int i = 1; i <= n; i++)
ans += iscut[i];
cout << ans << endl;
for (int i = 1; i <= n; i++)
if (iscut[i])
cout << i << " ";
return 0;
}AC记录
用 vector 存图的童鞋看这:
#include<bits/stdc++.h>
using namespace std;
const int N = 20010, M = 100010;
int n, m, dfn[N], low[N], cnt;
bool iscut[N];
vector<int> e[N];
void add_edge(int u, int v)
{
e[u].push_back(v);
e[v].push_back(u);
}
void tarjan(int u, int root)
{
dfn[u] = low[u] = ++cnt;
int sum = 0;
for (auto v : e[u])
{
if (!dfn[v])
{
sum++;//子节点+1
tarjan(v, root), low[u] = min(low[u], low[v]);
if (u != root && dfn[u] <= low[v]) iscut[u] = true;
}
else
low[u] = min(low[u], dfn[v]);
}
if (u == root && sum > 1) iscut[u] = true;
}
int main()
{
cin >> n >> m;
for (int i = 1, u, v; i <= m; i++)
scanf("%d%d", &u, &v), add_edge(u, v);
for (int i = 1; i <= n; i++)
if (!dfn[i])
tarjan(i, i);
int ans = 0;
for (int i = 1; i <= n; i++)
ans += iscut[i];
cout << ans << endl;
for (int i = 1; i <= n; i++)
if (iscut[i])
cout << i << " ";
return 0;
}

