树链剖分

树链剖分：shù liàn pōu fēn。
（为什么要写拼音因为总是拼成pō和pāo）。

思路

模板题：。

初步分析

这道题需要把树的路径当做区间修改。

所以区间修改你想到了什么？
没错，。

但是路径是不连续的，怎么区间修改。所以就需要多个连续区间赋值。

树链剖分

（网上找了张图，觉得挺好。）

重孩子、轻孩子和重链

首先我们需要知道重孩子、轻孩子和重链。
以下内容要求全文背诵。
重孩子：在自己父亲的孩子中孩子最多的。
轻孩子：不是重孩子就是轻孩子。
（注意：根节点是轻孩子）
重链：由一个轻孩子（根）和一些重孩子组成的一条链。
背诵吧。
注意：图中的重子节点和轻子节点就是重孩子和轻孩子。

分割连续区间

好的知道了重链，那如何分割出来连续区间呢？

首先，我们先给树打上 DFS 序。
然后，每条重链满足每个节点的编号是连续的。
那问题不就变为怎么把一条路径变为多个重链了吗？

遍历过程

所以那怎么把一条路径变为多个重链（废话连篇）。

例如我们遍历 14 和 19（分别 u,v）。

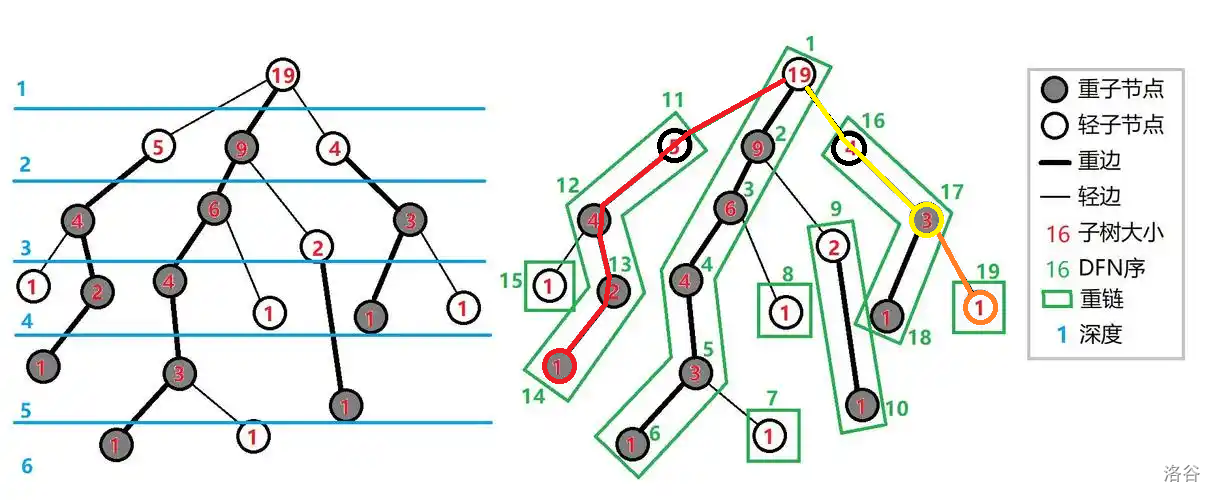
我们逐步分析：

1. 由于 14 更深，所以把 u 移动到重链顶端（11）然后再移动到父亲（1）。
2. 由于 19 更深，所以把 v 移动到重链顶端（没动）然后再移动到父亲（17）。
3. 由于 17 更深，所以把 v 移动到重链顶端（16）然后再移动到父亲（1）。
4. 相遇，遍历结束。

代码实现

预处理

我们需要 2 次 dfs，分别用于记录重孩子和打上 DFS 序。

具体讲解在注释里看吧。

void dfs1(int u, int f)//u：当前的编号，f:父亲节点
{
	dep[u] = dep[f] + 1;//记录深度
	fa[u] = f;//记录父亲
	siz[u] = 1;//初始化儿子数量
	int maxson = 0;//记录最重孩子编号
	for(int i = hd[u]; i; i = e[i].nxt)//遍历所有边
	{
		int v = e[i].v;
		if(v == f) continue;
		dfs1(v, u);//继续递归
		siz[u] += siz[v];//更新子节点数量
		if(siz[v] > maxson)//更新重孩子
			son[u] = v, maxson = siz[v];
	}
}
void dfs2(int u, int topf)//topf：这条重链的顶端
{
	id[u] = ++tot;//打上DFS序
	tw[tot] = w[u];//更新权值
	top[u] = topf;//记录
	if(!son[u]) return;//结束
	dfs2(son[u], topf);//递归重孩子
	for(int i = hd[u]; i; i = e[i].nxt)
	{
		int v = e[i].v;
		if(v == fa[u] || v == son[u]) continue;
		dfs2(v, v);//遍历轻孩子
	}
}

查找和赋值

int qyrange(int u, int v)
{
	int ans = 0;
	while(top[u] != top[v])
	{
		if(dep[top[u]] < dep[top[v]]) //让u更深
			swap(u, v);
		ans += query(1, 1, n, id[top[u]], id[u]);//增加
		ans %= mod;
		u = fa[top[u]]; 
	}
	if(dep[u] > dep[v]) swap(u, v);
	ans += query(1, 1, n, id[u], id[v]);
	ans %= mod;
	return ans;
}

void uptrange(int u, int v, int k)
{
	k %= mod;
	while(top[u] != top[v])
	{
		if(dep[top[u]] < dep[top[v]]) 
			swap(u, v);
		update(1, 1, n, id[top[u]], id[u], k);
		u = fa[top[u]]; 
	}
	if(dep[u] > dep[v]) swap(u, v);
	update(1, 1, n, id[u], id[v], k);
}